杨辉三角形（JAVA）

题目：

下面的图形是著名的杨辉三角形：

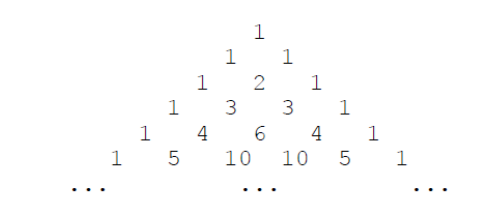
如果我们按从上到下、从左到右的顺序把所有数排成一列，可以得到如下数列：1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,⋯

给定一个正整数 N，请你输出数列中第一次出现 N 是在第几个数？

输入描述
输入一个整数 N。

输出描述
输出一个整数代表答案。

输入输出样例
示例 1

输入

6

输出

13

评测用例规模与约定
对于 20% 的评测用例，1≤N≤10； 对于所有评测用例，1≤N≤1000000000。

运行限制
最大运行时间：1s
最大运行内存: 256M

思路：

首先我想到的是将杨辉三角形构建出来再进行查找，但N的最大值是1*10^9，经过亲身实践只能通过40%的用例

所以需要找规律

杨辉三角形：

需要考虑的部分：

其中6=c(2,4) 2=c(1,2)因为10^9>c(16,32)但10^9<c(17,34),所以在16列以内肯定能找到所有的数，有效数列是0-16列。又因为每一行都是从左到右递增，每一列都是从上到下递增，每个数字都可以表示为c(i,j)。所以我们可以从十六列开始，逐步往前找采用二分行的方式找到答案。

代码：

import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改
 
public class Main {
 public static void main(String[] args) {
        Scanner sc=new Scanner(System.in);
        long N=sc.nextLong();
        for (int k=16;k>=0;k--){
            long l = 2 * k, r = Math.max(N, l), mid=0;  //代码是根据其它博主的博客写的这里我的理解是从2*k行开始才有的第16列有效数据然后加上r（r的理解有些模糊）再用二分查在哪一行，第16列没有满足的值继续往前查。
            while (l <= r) {//对第k列二分查找行
                mid = l + (r - l) / 2;//二分行
                long x = f(mid, k,N);
                if (x == N)
                    break;
                else if (x > N)
                    r = mid - 1;
                else
                    l = mid + 1;
            }
            if (f(mid, k,N) == N)
            {//第mid行、第k列的数就是N
                System.out.println((mid + 1) * mid / 2 + k + 1);
                //杨辉三角形的行数符号公差为1的等差数列，故用等差数列求和公式
                //加上第几列再加上1（因为列从0开始）即可得出该数的位置
                break;
            }
        }
        sc.close();
 
        }
        public static long f(long a,int b,long N){   //求c（i，j）的值,也就是i行j列的值
            long res = 1;
            for (long i = a, j = 1; j <= b; i--, j++)
            {
                res = res * i / j;
                if (res > N )//如果中间结果超过N就直接返回
                    return res;
            }
            return res;
        }
        }